[물리 기반 시뮬레이션/PBD] 위치 기반 동역학(PBD) 소개

1. 기존 방식

기존에 동역학을 구현하는 방식은 각각의 입자의 2차 ODE를 1차 ODE 2개로 분리할 수 있다. 이 ODE에서 내부, 외부 힘을 적용하여 Euler's Method를 풀어낸뒤 다음 위치를 추정하여 추정한 위치로 이동한다. 하지만 이런 방식의 단점은 오차가 스텝 크기에 따라 달라지고 힘을 적용하는 방식이 많아지면 더욱 더 복잡해지는 것이 단점이다.

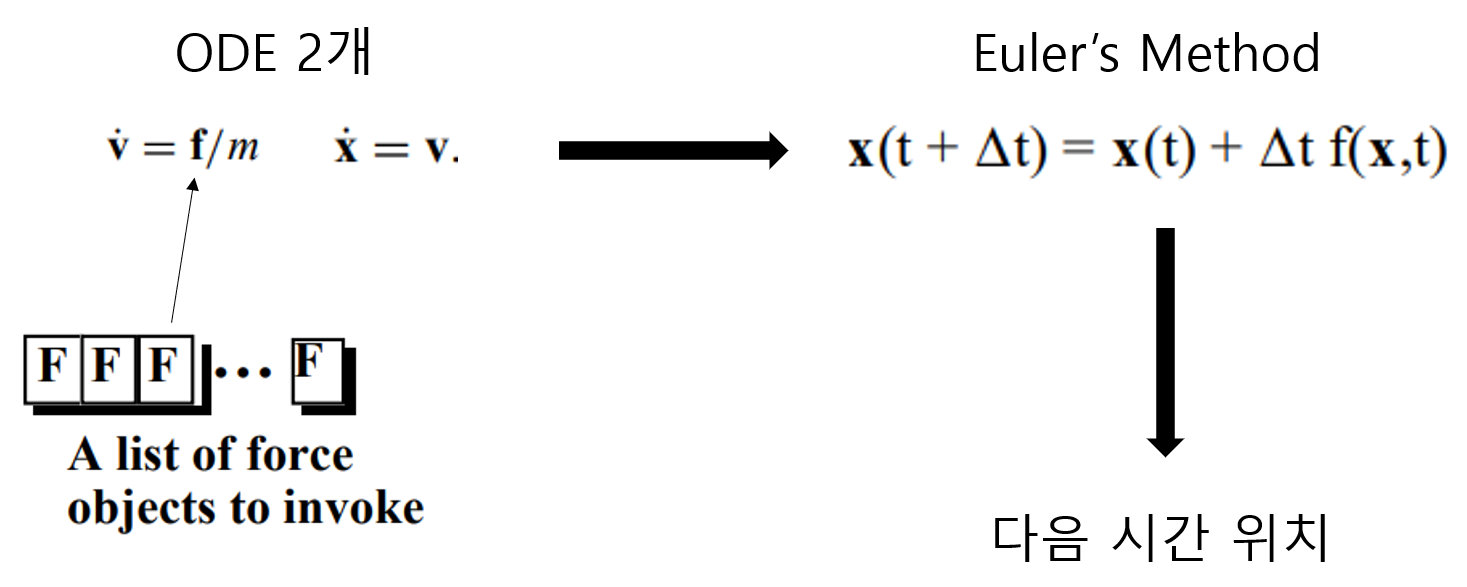
2. Position Based Dynamics란? (PBD)

Position Based Dynamics는 한국말로 위치 기반 동역학이고 앞의 Particle System Dynamics에서 다뤘듯이 입자의 위치와 속도를 사용자가 직접 할당해주는 방식이다. 직접 어떻게 할당을 할까? 기존 방식과 같이 Euler's Method를 적용하는 것 까진 똑같이 진행이 된다. 그러나 힘을 적용할 땐 외부 힘만 적용을 한다. 그리고 Euler's Method로 다음 시간 위치를 추정한 추정값에 제약조건을 적용하여 추정값을 수정한다. 이때 내부힘이 적용된다. 그리고 수정된 값으로 위치와 속도를 다시 할당해주면 다음 시간의 위치를 정해줄 수 있다.

3. PBD 기본 알고리즘

이 수도 코드는 PBD의 기본적인 알고리즘이다. 우선 1~3번 줄에서는 각 정점에 대한 초기값을 할당해준다. 그리고 4~17번줄에서 계속 반복하면서 PBD를 수행한다. 반복문에 들어가서 5번 줄에서 외부 힘을 적용하고 Euler's Method를 이용하여 v' = f/m 미분방정식을 풀어서 다음 시간에서의 속도를 추정한다. 그리고 시스템의 안정을 위해 6번 줄에서 dampVelocities에서 속도에 대한 Damping을 적용해준다. 그리고 7번 줄에서 Euler's Method를 이용하여 x' = v 미분 방정식을 풀어서 다음 시간에서의 위치를 추정한 추정값을 할당해준다. 8번 줄에서는 충돌에 대한 제약조건을 생성해준다. 9~11번 줄이 PBD를 풀어내는 핵심 Solver이다. Solver는 사용자가 지정한 횟수만큼 반복된다. 그리고 해당 반복문 안에서 ProjectConstraints에서 제약조건을 추정한 위치에 적용하여 위치를 보정해준다. 그 다음 12~15번 줄은 보정한 위치를 각 정점의 위치와 속도에 공식에 따라 할당해준다. 그리고 16번 줄은 마찰, 반발력에 의한 속도를 수정해준다. 이때 이 방식의 장점은 오차가 스텝크기에 의존하지 않고 solver의 반복 횟수에 의존하게 되고 내부 힘을 간단한 제약조건으로 표현할 수 있다는 점이 장점이다.

4. Solver

solver는 위의 알고리즘에서 9~11번 줄의 부분이다. solver의 입력으로는 M+Mcoli개의 제약 조건과 정점의 추정값인 P1, ..., Pn이다. 그리고 추정값을 보정하여 제약 조건을 만족시키도록 한다. 이를 적용하기 위해 Gauss-Seidel Method를 사용하는데 Gauss-Seidel Method는 선형 연립 방정식을 푸는 방식인데 제약조건에 대한 방정식은 비선형 방정식이 되기 때문에 이 방법에선 제약조건을 반복적으로 수행하면서 오차를 줄여가는 방식을 채택하게 된다. 

5. Constraint Projection

제약조건을 점들에 투영하여 점들을 이동시켜서 제약조건에 만족시키는 것이 이 단계에서 하는 일이다. 이때 이러한 제약조건 들은 내부힘에 의한 내부 제약조건이기 때문에 운동량과 각 운동량이 보존되어야 한다. 둘의 보존은 다음과 같다.

이런 운동량 보존을 위반한다면 이는 외부힘으로 작용하게 된다. 내부 제약조건의 경우는 제약함수 C가 이동과 회전에 독립적이다. 이는 정점을 이동하거나 회전하더라도 제약함수는 바뀌지 않는다는 말이된다. 따라서 C의 gradient는 Rigid Body 처럼 동작하게 된다. 이때 모든 질량이 동일하다면 추정값 P의 보정값 delta P를 C의 gradient 방향으로 할당하면 운동량을 보존할 수 있다. 그리고 주어진 P에 대해 C에 대한 다음 값을 추정한 추정값은 다음과 같이 보정된다.

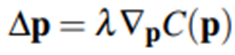
여기서 두 식을 정리하면 일반적인 정점 P에 대해 다음과 같이 식이 유도된다.

여기서 각 개별적인 Pi에 대해 식을 다시 정리하면 다음과 같다.

이는 각 정점 P가 동일한 질량을 가지고 있는 경우이다. 이때 정점 P가 개별 질량을 가지면 다음과 같이 유도된다.

그리고 하나의 예시를 들어서 이를 설명해보자 가장 간단한 예시인 spring system의 거리제약조건을 예시로 들어보면 다음과 같은 제약조건과 그림을 그릴 수 있다.

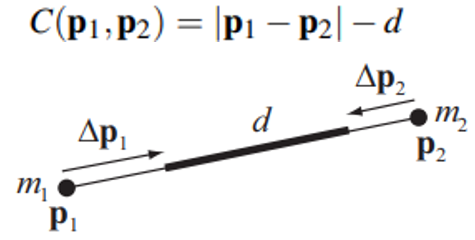
이때 공식에 모든 값을 대입해보면 P1과 P2에 대한 보정 값은 다음과 같이 유도된다.

마지막으로 Stiffness 즉, 강성계수에 대한 이야기를 해보면 강성계수를 가장 간단한 방식으로 적용하면 보정값에 그냥 계수 k를 곱해서 적용할 수 있다. 하지만 이렇게 적용을 하게 되면 오류가 반복횟수에 종속적으로 나오기 때문에 k를 어떤 식으로 바꿔서 바꾼 k'을 보정값에 곱해주면 오류가 반복횟수에 독립적으로 계수 k에 종속적으로 유도될 수 있다.

6. Collision

충돌을 감지하는 제약조건은 간단하게 만들면 매우 쉽게 만들 수 있다. 가장 간단한 예시는 평면과 정점의 충돌 감지인데 이때는 앞의 Particle System에서와 마찬가지고 평면위의 점에서 보정된 보정값까지의 벡터가 법선벡터와 내적했을 때 0보다 작으면 움직인 위치가 평면의 밑에 있기 때문에 다음 시간에 충돌이 일어난다는 말이 된다. 그리고 만약 충돌 감지를 실패했을 때는 이미 보정값을 제외한 기존 위치가 평면아래에 있으면 충돌 감지를 실패한 것이다. 이때의 제약 조건은 위에서 말한 내적값의 부등식으로 표현될 수 있고 이때 강성계수는 1이 된다.

다만 이 경우는 움직이는 정점과 가만히 있는 물체와의 충돌이다. 하지만 대부분의 경우는 두개의 움직이는 충돌체와의 충돌이다. 이때의 제약조건은 정점이 삼각형 메쉬를 통과했을때 정점을 삼각형의 위에 위치하도록 등식의 제약조건을 만들 수 있고 이를 수식으로 표현하면 다음과 같다.