[물리 기반 시뮬레이션/수치 해석] 미분 방정식의 기초 - Euler's method

1. 미분 방정식이란?

미분 방정식은 미지 함수와 그의 도함수들로 이루어진 방정식을 의미한다. 따라서 미분 방정식을 해결하면 함수를 얻어 낼 수 있다. 가장 일반적인 예시는 다음과 같다. (이는 상미분 방정식 즉, ODE의 예시이다.)

이를 2차원 벡터로 확장하여 Vector Field 에서의 미분방정식으로 확장하면 다음과 같이 나타낼 수 있다.

그림 1

2. Initial Value Problem

미분 방정식의 해를 구하는 방법은 매우 다양한 방식이 있는데 이 중 하나를 소개하려 한다. Initial Value Problem은 해석하면 초기 값 문제 즉, 초기 값이 주어진 상태에서 미분 방정식의 해를 구하는 방식이다. ODE를 풀다보면 적분상수가 생기기 때문에 특정 해를 구하기 어렵다 이떄 Initial Value가 주어지면 적분 상수를 풀 수 있기 때문에 ODE의 특정 해를 구할 수 있다. 예를 들면

다음과 같은 문제가 주어졌다고 했을 때 y를 모두 좌변으로 x를 모두 우변으로 정리한 후 양변에 dx를 곱하고 양변을 적분하면 적분 상수가 남게되고 y에 대해 식을 정리해도 특정 해를 구할 수 없다. 이때 y(0) = 0이라는 초기 값을 활용하면 특정 해를 구할 수 있다. 이를 그림 1 에서의 2차원 Vector Field로 확장해서 생각해보자 x(t)를 평면상의 한 점 p의 운동을 설명하는 함수라 하면 f(x, t)는 평면 상의 Vector Field로 정의 될 수 있다. 그러면 f는 x의 도함수이기 때문에 점 p가 x를 통과할 때 가지는 속도이다. 이때 initial value가 주어지면 초기 위치에서의 f가 결정되고 f는 속도이기 때문에 점 p의 다음시간 위치가 변화하게 된다. 따라서 p는 Vector Field를 따라서 궤적을 그리게 되고 이는 적분 곡선이다.

3. 수치 해석

수치 해석학이란 어떤 함수나 방정식의 해를 컴퓨터를 이용해 수치적으로 근사하여 근삿값을 구하는 방식에 대한 연구를 하는 학문이다. 따라서 위의 Vector Field 문제를 수치 해석적으로 바라보면 초기 값 x(t0)부터 시작하여 discrete한 시간에 관심이 있고 이는 미분을 이용하면 쉽게 할 수 있다.

4. Euler's Method

Euler's Method는 위의 Vector Field 문제를 수치 해석적으로 바라보는 가장 간단한 방법이다. 이는 진짜 적분 곡선을 추정할 수 있다. 초기 값 x(t0) 에서 시작하는 방정식은 discrete한 시간을 미분 방정식으로 정의할 수 있다. 이때 h는 discrete한 시간의 스텝 크기이다.

이러한 방식으로 적분 곡선을 추정해 나가서 시각화를 하면 매끄러운 곡선이 아닌 다각형의 각진 곡선으로 추정된다. Euler's Method는 간단한 만큼 오차가 큰 방법이다. 오차는 스텝의 크기인 h가 커질수록 커진다.

Euler's Method의 오차가 나는 예시로는 적분곡선이 원이 되는 경우에 점 p는 시간이 지나고 영원히 원을 공전해야 한다. 하지만 Euler's Method를 사용하면 오차가 누적되면서 점점 반지름이 더 큰 원을 중심으로 공전하게 된다. 따라서 최종적으로는 나선모양을 그리게 된다. 스텝의 크기를 줄이면 더 천천히 원을 이탈하게 되지만 오차를 0으로 만들 순 없다. 두번째 예시로는 불안정한 경우입니다. 1차원 함수 f = -kx에서 작은 크기의 스탭에서는 제대로 동작하지만 스탭의 크기가 1/k 이상이면 0을 중심으로 진동하고 2/k 이상이면 진동이 발산하게 된다. 이는 매우 불안정한 시스템이다.

Euler's method의 오류를 개선하기 위해서는 왜 오류가 생기는지에 대해 알아봐야 한다. 우선 Euler's method는 테일러 급수에 기반한다. 테일러 급수는 x(t0+h)를 무한한 도함수들의 합으로 표시할 수 있다.

하지만 Euler's method는 맨 앞 두 항만을 사용한다. 따라서 Euler's method가 오차가 없으려면 나머지 항들이 모두 0이 되도록 x(t)가 선형적인 경우에만 해당된다. 이 말은 오차가 테일러 급수의 무한함을 어디까지 계산할 수 있냐가 결정한다는 말이 된다. Euler's Method의 오차는 앞의 두 항을 뺀 것중 가장 앞의 항인 (h^2/2!)x''(t0) 에 의하여 결정되는데 여기서 변수는 h밖에 없으므로 오차는 O(h^2)으로 표시 가능하다. 즉, h를 절반으로 줄이면 오차는 1/4만큼만 발생한다는 뜻이 되어 오차가 줄어들게 된다. 따라서 이론적으로 Euler's method는 h를 줄여서 오류는 줄여나갈 수 있다.

5. Midpoint Method

Euler's method를 보완하고 개선할 수 있는 방법으로는 어떤 것이 있을까? 수많은 방법들 중에 하나가 바로 Midpoint method이다. 위의 문제에서 유도된 테일러 급수에서 2차항까지 계산할 수 있다면 오차는 O(h^2)에서 O(h^3)으로 줄일 수 있다. 

함수 f가 x에 간접적으로 의존한다고 가정하면 x' = f(x(t))가 된다. 이때 체인 룰을 적용하여 미분해보면

가 나오게 된다. 이때 함수 f의 테일러 급수를 구해보고 델타 x를 h/2f(x0)로 가정하면

이런 결과가 나오게 된다. f'f는 아까 계산한 미분에 의하여 x''로 유도된다.양변에 h를 곱하고 식을 정리하면 다음과 같다.

여기서 f(x0)는 f(x(t0))이기 때문에 x'(t0)로 유도되는 것을 볼 수 있다. 왼쪽항이 맨위의 오른쪽항과 같기 때문에 대입을 시키면

다음과 같이 계산된다. 이 결과 값은 2차항까지 계산한 값이므로 O(h^3)의 오차를 가진다. 이를 정리하면 먼저 Euler 스텝을 계산하고 스텝의 중간 지점에서 fmid를 계산하고 최종적으로 fmid를 이용하여 다음 위치를 업데이트 시킨다. 이 방법은 오차는 더 적지만 두번의 계산이 필요하다. 이를 그림으로 나타내면 다음과 같다.

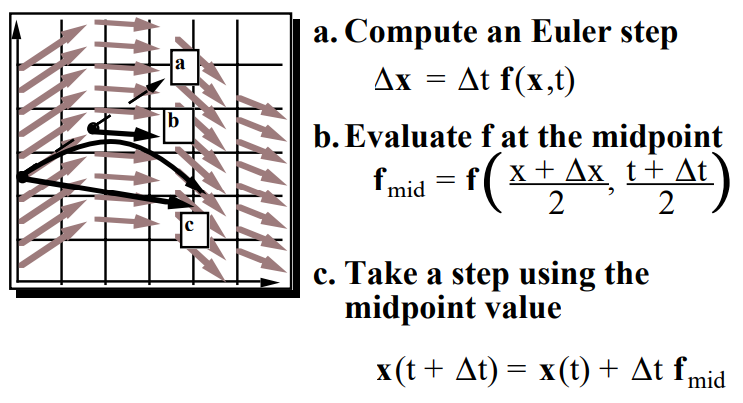
Midpoint method는 2차 솔루션이다. Euler's method의 오차를 줄이기 위해서는 3차, 4차 솔루션을 제시할 수 있고 하지만 계산량이 늘어난다는 단점이 있다. 이 중 가장 대표적인 경우는 4차 Runge-kutta method이다.

6. Step 크기 설정

Euler's method에서는 오차를 줄이는 것이 관건인데 오차는 h에 의해서 결정되기 때문에 h를 몇으로 설정하는 지가 중요한 부분이다. h를 한없이 작게하면 물론 오차도 줄이고 좋겠지만 계산량의 한계가 있기 때문에 적절한 h를 선택하는 것이 중요하다. 예를 들어 h의 스텝크기를 가지는 Euler's method의 오차가 xa, h/2의 스텝크기를 두번 수행한 오차가 xb라 하면 현재 오차 측정값은 다음과 같다.

예를 들어 허용할 수 있는 오차가 10^-4이고 현재 오차가 10^-8이면 자원이 낭비되고 있는 것이기 때문에 h를 늘릴 필요가 있다. 그리고 오차는 O(h^2)이므로 다음과 같이 100배 증가시키면 된다.

반대로 허용 오차가 10^-4이고 현재 오차가10^-3이면 오차가 너무 크기때문에 오차를 감소시켜야된다.

7. 실제 구현

실제로 Euler's method를 구현하는 것은 어렵지 않다 하지만 x Vector가 몇차원인지는 주어지기 전까지 모르기 때문에 모든 타입에 대해 대응해야 하는데 OOP 언어에서는 이를 generic 함수를 이용하면 쉽게 구현이 가능하다. 게임 분야에서 사용하는 대표적인 OOP언어 중 하나인 C#을 이용해 예시로 구현을 해보면

using System;

public class EulerMethod<T>
{
    public delegate T ODEFunction(T x, double t);

    public static T Solve(ODEFunction f, T x0, double t0, double h, double targetError)
    {
        double t = t0;
        T x = x0;

        while (t < 1.0)  // 예시로 t < 1.0까지 수행하도록 설정
        {
            T xa = Add(x, Multiply(f(x, t), h));  // 현재 step size로 Euler step 계산
            T xb = Add(x, Multiply(f(Add(x, Multiply(f(x, t), h / 2.0))), h / 2.0));  // 현재 step size의 절반으로 두 번의 Euler step 계산

            double error = SubtractMagnitude(xa, xb);  // 현재 step size의 오차 계산

            if (error <= targetError)
            {
                x = xa;  // 오차가 목표 오차 이내인 경우 x 업데이트
                t += h;  // t 업데이트
            }

            h *= Math.Sqrt(targetError / error);  // step size 조정
        }

        return x;
    }

    // 두 값의 합을 반환하는 제네릭 함수
    private static T Add(T a, T b)
    {
        dynamic da = a;
        dynamic db = b;
        return da + db;
    }

    // 값과 스칼라의 곱셈을 반환하는 제네릭 함수
    private static T Multiply(T value, double scalar)
    {
        dynamic dv = value;
        return dv * scalar;
    }

    // 두 값의 차이의 절대값을 반환하는 제네릭 함수
    private static double SubtractMagnitude(T a, T b)
    {
        dynamic da = a;
        dynamic db = b;
        return Math.Abs(da - db);
    }
}

// 예시로 x' = x + t를 사용하는 ODE 함수
public static class MyFunction
{
    public static double Evaluate(double x, double t)
    {
        return x + t;
    }
}

class Program
{
    static void Main(string[] args)
    {
        double x0 = 0.0;         // 초기 조건
        double t0 = 0.0;
        double h = 0.1;          // 초기 step size
        double targetError = 1e-4;  // 목표 오차

        double result = EulerMethod<double>.Solve(MyFunction.Evaluate, x0, t0, h, targetError);

        Console.WriteLine("Result: " + result);
    }
}

하지만 non-OOP 언어에서는 generic 함수를 이용할 수 없기 때문에 void 포인터와 함수 포인터를 이용하여 동적으로 타입을 할당할 수 있다. 가장 대표적인 non-OOP언어인 C를 이용해 예시로 구현은 해보면

#include <stdio.h>
#include <math.h>

typedef double (*ODEFunction)(double, double);  // ODE를 정의하는 함수 포인터 타입

void* eulerMethod(ODEFunction f, void* x0, double t0, double h, double targetError, size_t dataSize) {
    double t = t0;
    void* x = x0;

    while (t < 1.0) {  // 예시로 t < 1.0까지 수행하도록 설정
        void* xa = malloc(dataSize);
        void* xb = malloc(dataSize);

        // 현재 step size로 Euler step 계산
        for (size_t i = 0; i < dataSize / sizeof(double); i++) {
            double* xi = (double*)((char*)x + i * sizeof(double));
            double* xai = (double*)((char*)xa + i * sizeof(double));
            *xai = *xi + h * f(*xi, t);
        }

        // 현재 step size의 절반으로 두 번의 Euler step 계산
        for (size_t i = 0; i < dataSize / sizeof(double); i++) {
            double* xi = (double*)((char*)x + i * sizeof(double));
            double* xbi = (double*)((char*)xb + i * sizeof(double));
            *xbi = *xi + (h / 2.0) * f(*xi + (h / 2.0) * f(*xi, t), t + (h / 2.0));
        }

        double error = 0.0;

        // 현재 step size의 오차 계산
        for (size_t i = 0; i < dataSize / sizeof(double); i++) {
            double* xai = (double*)((char*)xa + i * sizeof(double));
            double* xbi = (double*)((char*)xb + i * sizeof(double));
            error += fabs(*xai - *xbi);
        }

        if (error <= targetError) {
            // 오차가 목표 오차 이내인 경우 x 업데이트
            for (size_t i = 0; i < dataSize / sizeof(double); i++) {
                double* xi = (double*)((char*)x + i * sizeof(double));
                double* xai = (double*)((char*)xa + i * sizeof(double));
                *xi = *xai;
            }

            t += h;  // t 업데이트
        }

        h *= sqrt(targetError / error);  // step size 조정

        free(xa);
        free(xb);
    }

    return x;
}

// 예시로 x' = x + t를 사용하는 ODE 함수
double myFunction(double x, double t) {
    return x + t;
}

int main() {
    double x0 = 0.0;         // 초기 조건
    double t0 = 0.0;
    double h = 0.1;          // 초기 step size
    double targetError = 1e-4;  // 목표 오차

    double result = *(double*)eulerMethod(myFunction, &x0, t0, h, targetError, sizeof(double));

    printf("Result: %f\n", result);

    return 0;
}

다음과 같이 구현할 수 있다. 목표로 설정한 오차는 10^-4로 설정하였다.